Definitivamente, não basta ter um quadro-negro, giz, carteiras e livros na sala de aula. Esses elementos já não são suficientes para educar e prender a atenção dos alunos.
"Crianças e adolescentes estão ávidos pelas tecnologias digitais. Vivem imersos nelas. Deixar de incluir no currículo escolar uma linguagem que faz parte do dia a dia deles desestimula a aprendizagem", afirma Sonia Bertocchi, mestre em gestão e produção de educação a distância, na Universidade Carlos III, de Madri. Modificar a estrutura de ensino que há décadas permanece engessada nas escolas, no entanto, é tarefa das mais complexas. "No mundo todo crescem as discussões sobre como inserir essas tecnologias na educação e, ainda, em que medida elas podem melhorar a qualidade do ensino", diz o professor Sérgio Gotti, diretor de formulação de conteúdos educacionais do Ministério da Educação (MEC).
No Brasil, o que se fez até hoje representa um tímido começo. A partir de 1997, o Ministério da Educação (MEC) começou a distribuir computadores na rede pública de ensino, por meio do Programa Nacional de Informática na Educação (ProInfo). Mas, de lá para cá, apenas 41% das escolas foram equipadas. Diante da crescente demanda, no ano passado, o MEC conseguiu, do Banco Nacional do Desenvolvimento (BNDES), um crédito de 650 milhões de reais para que governos municipais e estaduais pudessem adquirir computadores. Funcionou.
 Em apenas um ano 150 mil notebooks foram comprados. "Porém, não adianta apenas distribuí-los nas escolas sem preparar o professor para utilizá-los pedagogicamente", afirma Gotti.
Em apenas um ano 150 mil notebooks foram comprados. "Porém, não adianta apenas distribuí-los nas escolas sem preparar o professor para utilizá-los pedagogicamente", afirma Gotti.Justamente por isso, a partir de 2008, o ProInfo assumiu a tarefa de oferecer cursos que ensinem os educadores a dominar essas tecnologias e, principalmente, que os estimulem a usá-las em sala de aula. Muitos ainda preferem continuar "depositando" conteúdo nos estudantes sem buscar qualquer interação. "Se a atitude desse professor não mudar, mesmo que ele adote os meios digitais, vai usá-los de forma inadequada, reproduzindo no computador a velha prática de copiar e colar que usava nos livros", diz Jaciara de Sá, doutoranda em educação pela Universidade de São Paulo (USP) e autora do livro Redes e Comunidade, Ensino - Aprendizagem pela Internet (Instituto Paulo Freire).

Equipamentos e boa vontade de professores e diretores são um ótimo começo, mas não bastam. É necessário dar às escolas acesso à banda larga, mais rápida do que a internet discada, que ainda prevalece na rede pública. Segundo Sérgio Gotti, apenas 29% das escolas do país possuem acesso à internet. A maioria dos alunos continua acessando a rede de casa ou das lan houses, o que significa risco de receber informações incorretas e fazer mau uso do sistema.
Em meio a tantos obstáculos, é um alento conhecer alguns projetos que provam como é possível realizar essa transição a um custo razoável e com lucro certo. São histórias emocionantes que merecem aplausos.
Fonte: Blog de Consciência
A integração entre as tecnologias de informação e comunicação (TICs) e a educação deve se dar em duas dimensões indissociáveis (BELLONI, 2005, p. 9): como ferramenta pedagógica e como objeto de estudo.

Lendo o texto de MÍDIA-EDUCAÇÃO NO CONTEXTO ESCOLAR: MAPEAMENTO CRÍTICO DOS TRABALHOS REALIZADOS NAS ESCOLAS DE ENSINO FUNDAMENTAL EM FLORIANÓPOLIS PEREIRA, Silvio da Costa – UFSC, vê-se claramente o quão é importante esta inserido nas mudanças de recursos audio-visuais. O professor tem de refletir e achar novos meios de usar esses recursos ao seu favor.
Esse no entanto se torna o grande alvo de nossos trabalhos, ensinar como se fôsse uma atualização do facebook. Algo que gere curiosidade como as olimpíadas de Jogos On line e Educação - OJE. Que os faça ver as ferramentas on line como objeto de estudo e não uma poluição visual, ou mesmo um ato corriqueiro.
Necessitamos dar um f5 no currículo e vermos o novo aliado a TECNOLOGIA!
Esse no entanto se torna o grande alvo de nossos trabalhos, ensinar como se fôsse uma atualização do facebook. Algo que gere curiosidade como as olimpíadas de Jogos On line e Educação - OJE. Que os faça ver as ferramentas on line como objeto de estudo e não uma poluição visual, ou mesmo um ato corriqueiro.
Necessitamos dar um f5 no currículo e vermos o novo aliado a TECNOLOGIA!






 ,
,  ,
, ,
, ,
, .
. ,
, ,
, ,
, ,
, .
. ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
, .
. , onde
, onde  .
. .
. .
. .
.





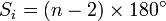
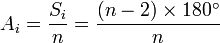










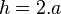



![d+={h \over sen[\frac{A_i .(n-1)}{2 .(n-2)}]}](http://upload.wikimedia.org/math/4/e/3/4e3e0e0575d71fabd797175a9f30d6cc.png)
![d-={l .sen(A_i) \over sen[\frac{A_i}{(n-2)}]}](http://upload.wikimedia.org/math/1/c/b/1cbb1a6f4a0c91383e4851610fbb52b5.png)