Polígono
Linhas poligonais e polígonos
Linha poligonal é uma sucessão de segmentos consecutivos e não-colineares, dois a dois. Classificam-se em:Polígono é uma superfície plana limitada por linhas rectas (lados). Um polígono divide o plano em que se encontra em duas regiões (a interior e a exterior), sem pontos comuns. Um polígono estrelado é uma linha poligonal fechada não-simples com propriedades especiais.
Elementos de um polígono
Um polígono possui os seguintes elementos:— Lados: Cada um dos segmentos de reta que une vértices consecutivos:
— Vértices: Ponto de encontro de dois lados consecutivos:,
,
,
,
.
A, B, C, D, E.— Diagonais: Segmentos que unem dois vértices não consecutivos:
 ,
, ,
, ,
, ,
,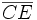 .
.— Ângulos internos: Ângulos formados por dois lados consecutivos:
— Ângulos externos: Ângulos formados por um lado e pelo prolongamento do lado a ele consecutivo:,
,
,
,
,
,
,
,
.
Classificação dos polígonos quanto ao número de lados
| Número de lados | Polígono |
|---|---|
| 3 | triângulo |
| 4 | quadrilátero |
| 5 | pentágono |
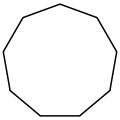
| 6 | hexágono |
| 7 | heptágono |
| 8 | octágono |
| 9 | eneágono |
| 10 | decágono |
| 11 | undecágono |
| 12 | dodecágono |
| 13 | tridecágono |
| 14 | tetradecágono |
| 15 | pentadecágono |
| 16 | hexadecágono |
| 17 | heptadecágono |
| 18 | octodecágono |
| 19 | eneadecágono |
| 20 | icoságono |
| 25 | pentacoságono |
| 30 | triacontágono |
| 40 | tetracontágono |
| 50 | pentacontágono |
| 60 | hexacontágono |
| 70 | heptacontágono |
| 80 | octacontágono |
| 90 | eneacontágono |
| 100 | hectágono |
| 1000 | quilógono |
| 1.000.000 | megágono |
| 109 | gigágono |
| 10100 | googólgono |
Nomeando polígonos
Para se construir o nome de um polígono com mais de 20 lados e menos de 100 lados, basta se combinar os prefixos e os sufixos a seguir:| Dezenas | e | Unidades | sufixo | ||
|---|---|---|---|---|---|
| -kai- | 1 | hena- | -gono | ||
| 20 | icosi- | 2 | -di- | ||
| 30 | triaconta- | 3 | -tri- | ||
| 40 | tetraconta- | 4 | -tetra- | ||
| 50 | pentaconta- | 5 | -penta- | ||
| 60 | hexaconta- | 6 | -hexa- | ||
| 70 | heptaconta- | 7 | -hepta- | ||
| 80 | octaconta- | 8 | -octa- | ||
| 90 | enneaconta- | 9 | -enea- | ||
| Dezenas | e | Unidades | sufixo | nome completo do polígono |
|---|---|---|---|---|
| tetraconta- | -kai- | -di- | -gono | tetracontakaidigono |
| Dezenas | e | Unidades | sufixo | nome completo do polígono |
|---|---|---|---|---|
| pentaconta- | -gono | pentacontagono | ||
Classificação dos polígonos
A classificação dos polígonos pode ser ilustrada pela seguinte árvore:Polígono
/ \
Simples Complexo
/ \
Convexo Côncavo
/ \ Não-ConvexosInscritível
/
RegularPropriedades dos polígonos convexos
- O número de vértices é igual ao número de lados.
- De cada vértice de um polígono de n lados, saem n − 3 diagonais (dv).
- O número de diagonais (d) de um polígono é dado por
 , onde n é o número de lados do polígono.
, onde n é o número de lados do polígono. - A soma das medidas dos ângulos internos de um polígono de n lados (Si) é dada por
 .
. - A soma das medidas dos ângulos externos de um polígono de n lados (Se) é igual a
 .
. - Em um polígono convexo de n lados, o número de triângulos formados por diagonais que saem de cada vértice é dado por n − 2.
- A medida do ângulo interno de um polígono regular de n lados (ai) é dada por
 .
. - A medida do ângulo externo de um polígono regular de n lados (ae) é dada por
 .
. - A soma das medidas dos ângulos centrais de um polígono regular de n lados (Sc) é igual a
 .
. - A medida do ângulo central de um polígono regular de n lados (ac) é dada por
 .
.
Outros polígonos
Alguns polígonos são diferente dos outros, por apresentarem lados cruzados, são eles:Estrelado
- Falso: Pela sobreposição de Polígonos
- Verdadeiro: Formado por linhas poligonais fechadas não-simples
Entrecruzado
Polígono, cujo prolongamento dos lados, ajudam a formar outro polígono.Ângulos de um Polígono Regular
Polígono Regular: É o polígono que possui todos os lados congruentes e todos os ângulos internos congruentes.Para um polígono de n lados, temos que a soma dos ângulos internos (S¡) =

Exemplos: Hexágono Regular: 6 lados Cálculo da Soma das medidas dos ângulos internos: S¡ = (6-2) . 180° = 4.180° = 720°
Como o Hexágono é regular: A¡ = 720º/6 = 120° Ae = 180º - 120º = 60°
O ângulo interno mede 120° e o externo, 60°.
Polígono regular
Índice[esconder] |
[editar] Formulário
Para um polígono regular de n lados, e medida de lado l:[editar] Soma dos Ângulos Internos (Si)
A soma dos ângulos internos de um polígono convexo regular pode ser calculada dividindo-se a figura com segmentos que ligam um vértice definido a cada um dos outros. O polígono será dividido em n − 2 triângulos, cada um com ângulo interno de 180° ou π radianos. Somando, encontra-se Si- Si = (n − 2)π
[editar] Ângulos Internos (Ai)
Um ângulo interno é aquele formado entre dois lados consecutivos. Num polígono regular, sendo todos os ângulos congruentes, pode ser obtido dividindo-se a soma dos ângulos internos pelo número de lados.[editar] Ângulos Externos (Ae)
São os suplementos dos ângulos internos:[editar] Raio (r)
Distância do vértice do polígono até o seu centro. Também é o raio de uma circunferência cincunscrita ao polígono.[editar] Apótema (a)
Distância perpendicular de um dos lados do polígono até o seu centro. Também é o raio de uma circunferência inscrita no polígono.[editar] Altura (h)
Em um polígono com número par de lados, é a distância perpendicular entre 2 lados opostos. Já em um polígono com número ímpar de lados, é a distância perpendicular entre um lado e seu vértice oposto.- Se n é par:
- Se n é ímpar:
[editar] Diagonais (d)
Distância entre 2 vértices não-consecutivos do polígono (ou seja, as fórmulas referentes a diagonais não se aplicam a triângulos). Fórmula: n(n - 3) / 2[editar] Diagonal principal (dp)
Distância entre 2 vértices opostos do polígono. Só existe caso o polígono tenha um número par de lados.- Se n é par:
[editar] Maior diagonal (d+)
Maior distância entre 2 vértices do polígono. Em um polígono com número par de lados é a diagonal principal.- Se n é ímpar e maior que 3:
[editar] Menor diagonal (d-)
Menor distância entre 2 vértices do polígono.- Para n maior que 3:
[editar] Número de diagonais (Nd)
[editar] Número de diagonais de um UNICO VÉRTICE
O número de diagonais que se pode obter de um vértice é- ND = (n − 3)
[editar] Perímetro (2P)
Soma da medida dos lados.[editar] Semiperímetro (p)
Semiperímetro é a medida da metade do perímetro de uma figura geométrica[editar] Área (A)
Superfície ocupada pelo polígono.
- A = p.a







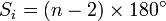
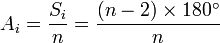










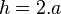



![d+={h \over sen[\frac{A_i .(n-1)}{2 .(n-2)}]}](http://upload.wikimedia.org/math/4/e/3/4e3e0e0575d71fabd797175a9f30d6cc.png)
![d-={l .sen(A_i) \over sen[\frac{A_i}{(n-2)}]}](http://upload.wikimedia.org/math/1/c/b/1cbb1a6f4a0c91383e4851610fbb52b5.png)
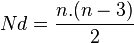


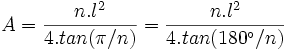


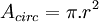


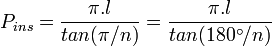



Nenhum comentário:
Postar um comentário